10.2. Exercise 2 Solutions#
#4.3.5 Exercise 1
#Using Cantera, determine the specific volume (𝑣) of water vapor where 𝑝 = 8 bar and 𝑇 = 200 ∘ C. What about 𝑇 = 220 ∘ C?
#Using Cantera:
import cantera as ct
#define state 1 as water
species1=ct.Water()
#define pressure in Pa
P1=800*1000
#define temperature in K
T1=200+273.15
species1.TP=T1,P1
print(f"Specific volume using Cantera: {round(species1.PV[1],2)} m^3/kg")
T2=220+273.15 #redefine T to be 220 C
species1.TP=T2,P1
print(f"At 220 \N{DEGREE SIGN}C, specific volume using Cantera: {round(species1.PV[1],2)} m^3/kg")
Specific volume using Cantera: 0.26 m^3/kg
At 220 °C, specific volume using Cantera: 0.27 m^3/kg
#4.3.5 Exercise 2
# What is the composition (compressed, saturated, superheated) and pressure of H2O with 𝑣 = 65 m3 kg-1 and T = 15 ∘ C? What is the quality, x (if applicable)? Use Cantera to solve.
#Using Cantera:
import cantera as ct
#define state 1 as water
species1=ct.Water()
#define specific volume in m3/kg
v=65 #m3/kg
#define temperature in K
T=15+273.15
species1.TV=T,v
print(species1())
print(f"Pressure using Cantera: {round(species1.PQ[0],2)} Pa")
print(f"Phase: {species1.phase_of_matter}")
print(f"Phase is saturated with a quality of: {round(species1.PQ[1],2)}")
water:
temperature 288.15 K
pressure 1701.6 Pa
density 0.015385 kg/m^3
mean mol. weight 18.016 kg/kmol
vapor fraction 0.83244
phase of matter liquid-gas-mix
1 kg 1 kmol
--------------- ---------------
enthalpy -1.3855e+07 -2.4961e+08 J
internal energy -1.3966e+07 -2.5161e+08 J
entropy 10868 1.958e+05 J/K
Gibbs function -1.6987e+07 -3.0603e+08 J
heat capacity c_p inf inf J/K
heat capacity c_v nan nan J/K
None
Pressure using Cantera: 1701.64 Pa
Phase: liquid-gas-mix
Phase is saturated with a quality of: 0.83
#4.3.5 Exercise 3
# What is the composition (compressed, saturated, superheated) and temperature of H2O with 𝑣 = 1 m3 kg-1 and 𝑝 = 0.5 MPa? What is the quality, x (if applicable)? Use Cantera to solve.
#Using Cantera:
import cantera as ct
#define state 1 as water
species1=ct.Water()
#define specific volume in m3/kg
v=1 #m3/kg
#define pressure in Pa
P=0.5*1000*1000
species1.PV=P,v
print(species1())
print(f"Temperature using Cantera: {round(species1.TQ[0],2)} K")
print(f"Phase: {species1.phase_of_matter}")
water:
temperature 1084.4 K
pressure 5e+05 Pa
density 1 kg/m^3
mean mol. weight 18.016 kg/kmol
vapor fraction 1
phase of matter supercritical
1 kg 1 kmol
--------------- ---------------
enthalpy -1.1787e+07 -2.1236e+08 J
internal energy -1.2287e+07 -2.2137e+08 J
entropy 12366 2.2278e+05 J/K
Gibbs function -2.5197e+07 -4.5394e+08 J
heat capacity c_p 2351.4 42363 J/K
heat capacity c_v 1886.8 33993 J/K
None
Temperature using Cantera: 1084.4 K
Phase: supercritical
#4.3.5 Exercise 4
# What is the composition (compressed, saturated, superheated) and pressure of H2O with 𝑣 = 1 m3 kg-1 and T = 150 ∘ C? What is the quality, x (if applicable)? Use Cantera to solve.
#Using Cantera:
import cantera as ct
#define state 1 as water
species1=ct.Water()
#define specific volume in m3/kg
v=1 #m3/kg
#define temperature in K
T=150+273.15
species1.TV=T,v
print(species1())
print(f"Pressure using Cantera: {round(species1.PQ[0],2)} Pa")
print(f"Phase: {species1.phase_of_matter}")
water:
temperature 423.15 K
pressure 1.9207e+05 Pa
density 1 kg/m^3
mean mol. weight 18.016 kg/kmol
vapor fraction 1
phase of matter gas
1 kg 1 kmol
--------------- ---------------
enthalpy -1.3201e+07 -2.3784e+08 J
internal energy -1.3393e+07 -2.413e+08 J
entropy 10819 1.9492e+05 J/K
Gibbs function -1.778e+07 -3.2032e+08 J
heat capacity c_p 2054.2 37008 J/K
heat capacity c_v 1536.7 27686 J/K
None
Pressure using Cantera: 192066.2 Pa
Phase: gas
#4.3.5 Exercise 5
#A rigid tank contains 50 kg of saturated liquid water at 90 ∘ C. Determine the pressure in the tank and the tank volume.
m = 50 # kg
T = 90+273.15 # K
x=0# saturated liquid
#Using Cantera:
import cantera as ct
#define state 1 as water
species1=ct.Water()
species1.TQ=T,x
#print(species1())
print(f"Pressure using Cantera: {round(species1.PQ[0],2)} Pa")
V = species1.PV[1]*m #m3
print(f"Volume is {round(V,3)} m^3")
Pressure using Cantera: 70042.36 Pa
Volume is 0.052 m^3
#4.3.5 Exercise 6
#Compare the specific volume of nitrogen (N2) at 35°C and 150 kPa using the ideal gas law and Cantera.
#In Cantera use ct.Nitrogen() rather than ct.Water() as we have been for H2O.
#Using the ideal gas law:
#define known values
#convert temperature to kelvin
T=35+273.15
P=150
M=28
def v_ideal(T,P,M):
return 8.314*T/(M*P)
print(f"Specific volume using Ideal Gas Law: {v_ideal(T,P,M)} m^3/kg")
#Using Cantera:
import cantera as ct
#define state 1 as nitrogen
species1=ct.Nitrogen()
#redefine pressure in Pa
P=150*1000
species1.TP=T,P
print(f"Specific volume using Cantera: {species1.PV[1]} m^3/kg")
Specific volume using Ideal Gas Law: 0.6099902619047619 m^3/kg
Specific volume using Cantera: 0.6096046212951401 m^3/kg
#4.3.5 Exercise 7
#given: CO2, pressure is 5 MPa, near the critical pressure (7.38 MPa), therefore cannot assume ideal gas behavior
#2a
#determine vf and vg of CO2 at 5MPa
species1=ct.CarbonDioxide()
#get saturated liquid (vf) values (quality=0)
species1.PQ=5000000,0
print(f"Saturated liquid value: {species1.PV[1]} m^3/kg")
#get saturated vapor (vg) values (quality=1)
species1.PQ=5000000,1
print(f"Saturated vapor value: {species1.PV[1]} m^3/kg")
Saturated liquid value: 0.0012052903896509952 m^3/kg
Saturated vapor value: 0.006414524448873753 m^3/kg
#7b
#What is the saturated temperature of CO2 at 5 MPa?
#can use either 1 or 0 for the quality- either one will yield the saturation temperature
species1.PQ=5000000,1
#print the saturation temperature
print(f"Saturated temperature of CO2 at 5 MPa: {species1.TV[0]} K")
Saturated temperature of CO2 at 5 MPa: 287.4532698240636 K
#7c
#Compare the specific volume of CO2 at 5 MPa at saturated vapor conditions using Cantera and the ideal gas law
#at the same Tsat and Psat.
#intuitively we know these should differ because CO2 does not exhibit ideal gas behavior at high pressures
#using Cantera
#saturated vapor, quality=1
species1.PQ=5000000,1
print(f"Saturated vapor value: {species1.PV[1]} m^3/kg")
satvap=species1.PV[1]
Tsat=species1.TV[0]
#using the Ideal Gas Law
#molar mass for CO2
M=44
#convert pressure to kPa
P=500
T=Tsat
def v_ideal(T,P,M):
return 8.314*T/(M*P)
print(f"Specific volume using ideal gas law: {v_ideal(T,P,M)} m^3/kg")
#as expected, these values differ by several orders of magnitude
Saturated vapor value: 0.006414524448873753 m^3/kg
Specific volume using ideal gas law: 0.1086312038780575 m^3/kg
#7d
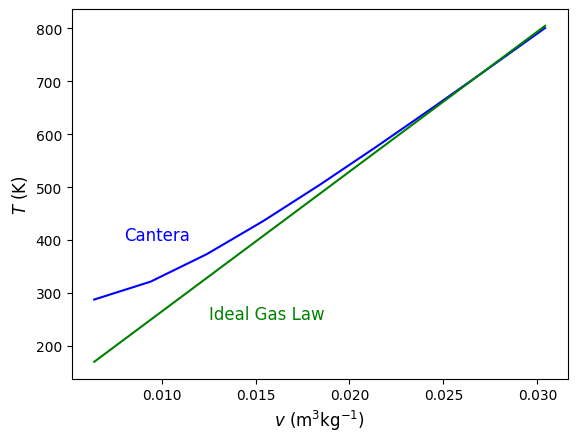
#Plot specific volume from the saturated vapor point at 5 MPa to 5 times vg at the same pressure.
#Use both Cantera and the ideal gas EOS.
#import relevant libraries
import numpy as np
import matplotlib.pyplot as plt
#using previously calculated vg
satvap=0.006414524448873753
P=5000000
species1.PQ=P,1
#create an array of specific volume values from vg @ 5 MPa to 5 times that
sv=np.arange(satvap,5*satvap,.003)
#create an empty array in which to hold the temperature values
T=[]
for i in sv:
species1.PV=[P,i]
T.append(species1.TP[0])
P=5000 #convert pressure to kPa
M = 44 # molecular weight of CO2
def T_ideal(P,sv,M):
return (P*sv)/(8.314/M)
Tideal=T_ideal(P,sv,M)
plt.plot(sv,T,color='blue')
plt.plot(sv,Tideal,color='green')
plt.xlabel('$v$ $(\mathrm{m^3} \mathrm{kg^{-1}})$', fontsize=12)
plt.ylabel('$T$ $({\mathrm{K})}$', fontsize=12)
plt.annotate('Cantera', (.008,400), color='Blue', rotation = 0,fontsize=12)
plt.annotate('Ideal Gas Law', (.0125,250), color='Green', rotation = 0,fontsize=12)
plt.show()
<>:27: SyntaxWarning: invalid escape sequence '\m'
<>:28: SyntaxWarning: invalid escape sequence '\m'
<>:27: SyntaxWarning: invalid escape sequence '\m'
<>:28: SyntaxWarning: invalid escape sequence '\m'
/tmp/ipykernel_1479/2263413414.py:27: SyntaxWarning: invalid escape sequence '\m'
plt.xlabel('$v$ $(\mathrm{m^3} \mathrm{kg^{-1}})$', fontsize=12)
/tmp/ipykernel_1479/2263413414.py:28: SyntaxWarning: invalid escape sequence '\m'
plt.ylabel('$T$ $({\mathrm{K})}$', fontsize=12)
#4.3.5 Exercise 8
#A 2.1 m3 rigid tank contains liquid-vapor mixture of H2O at 230°C. One-half of the volume is in the liquid phase and the rest is in the vapor form. Using Cantera, determine:
# a) the pressure of the steam,
# b) the quality of the saturated mixture, and
# c) the density of the mixture.
V = 2.1 # m3
T = 230+273.15 # K
Vf = 0.5*V
Vg = 0.5*V
#need to know mass of liquid and gas to determine quality. For this we can use vf and vg, recognizing V=m*v
#Using Cantera:
import cantera as ct
#define state 1 as water
species1=ct.Water()
species1.TQ=T,0
vf=species1.TV[1]
species1.TQ=T,1
vg=species1.TV[1]
mg=Vg/vg
mf = Vf/vf
x=mg/(mf+mg)
print("The quality is", round(x,3))
species1.TQ=T,x
print(f"Pressure: {round(species1.PQ[0],2)} Pa")
print(f"Density: {round(species1.DPQ[0],2)} kg/m3")
The quality is 0.017
Pressure: 2792630.52 Pa
Density: 420.62 kg/m3
#4.3.5 Exercise 9
#What is the specific volume of water at 5 MPa and 100°C? What would it be if the incompressible liquid approximation were used? Use Cantera to solve.
P = 5*1000*1000 # Pa
T = 100+273.15 # K
#Using Cantera:
import cantera as ct
#define state 1 as water
species1=ct.Water()
species1.TP=T,P
print(f"Real specific volume: {round(species1.TV[1],6)} m3/kg")
species1.TQ=T,0 #set quality to be zero at temperature of interest - different pressure
print(f"Incompressible assumption specific volume: {round(species1.TV[1],6)} m3/kg")
Real specific volume: 0.001041 m3/kg
Incompressible assumption specific volume: 0.001044 m3/kg
#4.3.5 Exercise 10
#Water initially at 200 kPa and 300°C is contained in a piston–cylinder device fitted with stops, State 1.
#a) The water is allowed to cool at constant pressure until it exists as a saturated vapor and the piston rests on the stops, State 2. Determine the change in specific volume during the process. Use Cantera to solve.
#b) Then the water continues to cool at constant volume until the pressure is 100 kPa, State 3. What is the temperature at State 3? Use Cantera to solve.
#part a
P1=P2 = 200*1000 # Pa, initial and final pressures in part a
T1 = 300+273.15 # K, initial temperature in part a
Q2 = 1 # Quality after it reaches the stops in part a
#Using Cantera:
import cantera as ct
#define state 1 as water at conditions of state 1
species1=ct.Water()
species1.TP=T1,P1
#and define state 2
species2=ct.Water()
species2.PQ=P2,Q2
print(f"Specific volume state 1: {round(species1.TV[1],6)} m3/kg")
print(f"Specific volume state 2: {round(species2.TV[1],6)} m3/kg")
print(f"Change in specific volume: {round(species2.TV[1]-species1.TV[1],6)} m3/kg")
#part b
P3 = 100*1000 # Pa, final pressure
v3=v2=species2.TV[1]
#and define state 3
species3=ct.Water()
species3.PV=P3,v3
print(f"Temperature state 3: {round(species3.TV[0],2)} K")
Specific volume state 1: 1.316165 m3/kg
Specific volume state 2: 0.885809 m3/kg
Change in specific volume: -0.430356 m3/kg
Temperature state 3: 372.81 K
#4.3.5 Exercise 11
# One kilogram of water fills a 150-L rigid container at an initial pressure of 2 MPa. The container is then cooled to 40°C.
# Determine the initial temperature and the final pressure of the water. Use Cantera to solve.
m1= 1 #kg, system mass
V1=150*.001 # m3, initial volume
v1 = v2= V1/m1 #m3/kg, initial an final specific volume because it is rigid and fixed mass
P1 = 2*1000*1000 # Pa, initial pressure
T2 = 40+273.15 # K, final temperature
#Using Cantera:
import cantera as ct
#define state 1
species1=ct.Water()
species1.PV=P1,v1
print(f"Initial temperature: {round(species1.TV[0],2)} K")
#define state 2
species2=ct.Water()
species2.TV=T2,v2
print(f"Final pressure: {round(species2.TP[1]/1000,2)} kPa")
Initial temperature: 668.36 K
Final pressure: 7.37 kPa
#4.3.5 Exercise 12
#A piston–cylinder device contains 0.6 kg of steam at 300°C and 0.5 MPa. Steam is cooled at constant pressure until one-half of the mass condenses.
# a) Determine the final temperature. Use Cantera to solve.
# b) Determine the change in volume. Use Cantera to solve
m = 0.6 # kg
mg = mf = 0.5*m # half of the mass condenses
T1 = 300+273.15 # K, initial temperature
P1 = P2 = 0.5*1000*1000 # Pa, initial pressure
Q2 = mg/m #quality after condensation
import cantera as ct
#define state 1
species1=ct.Water()
species1.TP=T1,P1
print(f"Initial specific volume: {round(species1.TV[1],2)} m3/kg")
#define state 2
species2=ct.Water()
species2.PQ=P2,Q2
print(f"Final temperature: {round(species2.TP[0],2)} K")
print(f"Final specific volume: {round(species2.TV[1],2)} m3/kg")
print(f"Change in volume: {m*round(species2.TV[1]-species1.TV[1],2)} m3/kg") #make sure to multiply by the mass
Initial specific volume: 0.52 m3/kg
Final temperature: 425.04 K
Final specific volume: 0.19 m3/kg
Change in volume: -0.198 m3/kg
#4.3.5 Exercise 13
#10 kg of R-134a fill a 1.115-m3 rigid container at an initial temperature of –30°C.
#The container is then heated until the pressure is 200 kPa.
#Determine the final temperature and the initial pressure.
import cantera as ct
import numpy as np
Kc = 273.15
# Given:
M = 10 # kg
V = 1.115 # m3
T1 = -30 + Kc
P2 = 200e3
# Find: T2, P1
v1 = V/M
v2 = v1
state1 = ct.Hfc134a()
state1.TV = T1, v1
state2 = ct.Hfc134a()
state2.PV = P2, v2
# final temperature
T2 = state2.TV[0]
# initial pressure
P1 = state1.PV[0]
print(f"The intial pressure is {round(P1/1000,2)} kPa, and final temperature is {round(T2-Kc,2)} C")
The intial pressure is 84.38 kPa, and final temperature is 14.18 C
#4.3.5 Exercise 14
#1 kg of R-134a fills a 0.14 m3 weighted piston cylinder device at -26.4 °C.
#The container is now heated until the temperature is 100 °C.
#Determine the final volume of the R-134a.
import cantera as ct
import numpy as np
Kc = 273.15
# Given:
M = 1 # kg
V1 = 0.14 # m3
T1 = -26.4 + Kc
T2 = 100 + Kc
state1 = ct.Hfc134a()
v1 = V1/M # get specific volume
state1.TV = T1,V1
P1 = state1.PV[0]
P2 = P1
state2 = ct.Hfc134a()
state2.TP = T2, P2
v2 = state2.TV[1]
print(f"The final volume is {round(v2,3)} m3")
The final volume is 0.302 m3
#4.3.5 Exercise 15
#Find the temperature, T, and specific volume, v, of a saturated vapor at 5 MPa
import cantera as ct
species1 = ct.Water()
#Saturated Vapor so the quality, Q = 1, anf given that P = 5 MPa = 5000000 Pa
species1.PQ = 5000000, 1
#Print results
print(f'The temperature T of the substance is {round(species1.TP[0],2)} K')
print(f'The specific volume, v, is {round(species1.PV[1],5)} kg/m\u00b3')
The temperature T of the substance is 537.18 K
The specific volume, v, is 0.03945 kg/m³
#4.3.5 Exercise 16
#Find the specific volume, v, at 1MPa and 5 MPa using the ideal gas law
#given T = 500 K and M = 44 kg/kmol
import cantera as ct
#ideal gas law: Pv = RT/M
T = 500
M = 44
def v_ideal_gas(P,T,M):
return (8314*T)/(P*M)
#1 MPa
v1 = v_ideal_gas(1000000,T,M)
#5 MPa
v2 = v_ideal_gas(5000000,T,M)
#print ideal gas specific volume approximations
print('Ideal gas approximation:')
print(f'At 1 MPa the specific volume is {round(v1,6)} kg/m\u00b3')
print(f'At 5 MPa the specific volume is {round(v2,6)} kg/m\u00b3')
#find using cantera
species1 = ct.CarbonDioxide()
#1 MPa
species1.TP = T, 10000000
v1 = species1.PV[1]
#5 MPa
species1.TP = T, 5000000
v2 = species1.PV[1]
print('Cantera approximation:')
print(f'At 1 MPa the specific volume is {round(v1,6)} kg/m\u00b3')
print(f'At 5 MPa the specific volume is {round(v2,6)} kg/m\u00b3')
Ideal gas approximation:
At 1 MPa the specific volume is 0.094477 kg/m³
At 5 MPa the specific volume is 0.018895 kg/m³
Cantera approximation:
At 1 MPa the specific volume is 0.008849 kg/m³
At 5 MPa the specific volume is 0.018237 kg/m³
#4.3.5 Exercise 17
#Find the pressure and quality at state 2
import cantera as ct
species1 = ct.Water()
P = 500000
V = 0.001
m = 0.0025
#find specific volume
v = V/m
print(f'The specific volume at state one is {v} kg/m\u00b3')
#set up with given values
species1.PV = P, v
#find the temperature at state one
T = species1.TP[0]
print(f'The temperature at state 1 is {round(T,2)} K')
#set up values for state 2 where T1 = T2 and v = v/3
species1.TV = T, v/3
P = species1.PQ[0]
Q = species1.PQ[1]
#Print results
print(f'The pressure at state 2 is {round(P/1000,2)} KPa')
print(f'The quality at state 2 is {round(Q,4)}')
The specific volume at state one is 0.4 kg/m³
The temperature at state 1 is 448.75 K
The pressure at state 2 is 903.9 KPa
The quality at state 2 is 0.6207
#4.3.5 Exercise 18
#Find the temperature at state one and the pressure at state 2
import cantera as ct
species1 = ct.Nitrogen()
#solve for specific volume
V = 0.005
m = 0.015
v = V/m
#Set up state one
species1.PV = 50000, v
#find the temperature
T1 = species1.TV[0]
print(f'The temperature at state 1 is {round(T1,2)} K')
#show state of matter
print(f'The substance at state 1 is a {species1.phase_of_matter}.')
#Set up state 2
T2 = T1 + 20
species1.TV = T2, v
#Find pressure
P2 = species1.PV[0]
print(f'The pressure at state 2 is {round(P2/1000,2)} KPa')
#show state of matter
print(f'The substance at state 2 is a {species1.phase_of_matter}.')
The temperature at state 1 is 71.75 K
The substance at state 1 is a liquid-gas-mix.
The pressure at state 2 is 80.04 KPa
The substance at state 2 is a gas.
#4.3.5 Exercise 19
#Find the mass inside the piston and the pressure after expansion
#State 1: given
import cantera as ct
species1 = ct.Water()
V1 = 0.000025 #m^3
T = 500
Q = 1
#State 1
species1.TQ = 500, 1
#find the mass
v = species1.PV[1]
m = V/v
print(f'The mass of water in the piston is {round(m,4)} kg')
#Set up state 2
V2 = V1*20
species1.TV = T, V2
#find the pressure at state 2
P2 = species1.PV[0]
#print pressure
print(f'The pressure at state 2 is {round(P/1000,2)} KPa')
The mass of water in the piston is 0.0659 kg
The pressure at state 2 is 903.9 KPa
