5. First Law of Thermodynamics - Introduction to Closed Systems#
5.1. Macroscopic and Microscopic Forms of Energy#
The total energy of a system (\(E\)), may be comprised of macroscopic and microscopic forms of energy. The macroscopic forms, such as kinetic energy (\(KE\)) and potential energy (\(PE\)), are measured with respect to an external reference frame. The \(KE\) of the system is related to it’s motion relative to an external reference frame, and the \(PE\) relative to its position as a result of gravity. Other external factors that contribute to the macroscopic energy of the system, such as magnetism, electricity and surface tension are typically ignored in introductory texts and only are applied in specialized cases. They are not considered further here. \(KE\) is related to the mass of the system and its velocity (\(V\)) by the equation below:
\(PE\) is related to the mass of the system, its height (\(z\)) and the acceleration due to gravity (\(g\)) the equation below:
where \(g\) = 9.8 \(\frac{\rm m}{\rm s^2}\)
Microscopic forms of energy include thermal energy, chemical energy and nuclear energy. These microscopic forms of energy are broadly related to the aggregate energy of the molecules and electrons in the system, for example due to kinetic energy of the molecules (i.e. translational energy), rotational and vibrational energy of the molecules, electron translation and rotation, atomic bonding and nuclear forces. For a more rigorous discussion refer to [Cengel et al., 2015]. The total microscopic energy contained in a system, which is combined of thermal, chemical and nuclear energy, is referred to as the internal energy (\(U\)). Therefore, we can mathematically express the total energy of a closed system as:
And the total specific energy as
where \(e\) = \(\frac{E}{m}\), \(ke\) = \(\frac{KE}{m}\), \(pe\) = \(\frac{PE}{m}\) and \(u\) = \(\frac{U}{m}\).
5.2. Energy Transfer and The First Law#
Energy transfer to or from a closed system is always in the form of heat transfer (\(Q\)) or work interactions (\(W\)). A discussion of the different types of heat transfer and work are discussed later below, but for now we will treat these terms generally in the context of energy conservation. The First Law of Thermodynamics states that energy is always conserved, and during a process, as it disaapears in one form, it reappears as another. This law, also referred to as the Conservation of Energy principle, is very general and can be applied to any system, so far as it has a clearly defined boundary. This law should not be interpreted to mean that the energy of a system cannot change, but rather that the change in energy of the system is equal to the net heat transfer or work applied to or extrated from the system. Take Count Rumford’s pioneering experiments (discussed initially in Section 3.1 Thermodynamic Systems) as an example [Thompson, 1798]. In these experiments, a paddle wheel was used to agitate an insulated system filled with liquid H2O - in other words, mechanical work was added to the system, the system being the insulated vessel. As a result of the work (i.e., energy) that was added to the system, the H2O eventually began to boil as a result. In the context of the First Law of Thermodynamics, this should be interpreted as, the change in energy of the H2O is equal to the work added to the system. Rumford’s experiments helped establish the First Law and explain the rationale for the portion of the statement “…as it disaapears in one form, it reappears as another”. But it wasn’t until Joule’s more precisly conducted measurements half a century later in 1850 that the premise of “energy is always conserved” was established [Joule, 1850]. This was confirmed with a similar paddle wheel experiment to Rumford, but with more precise measurements of the mechanical work applied to the system and the corresponding temperature changes. The precise temperature measurements, which were critical to the interpretation of the experimental data, were attributed to Joule’s expertise in beer brewing.
Combining the fact that energy transfer to or from a closed system always occurs via heat or work interactions, with the conservation of energy principle, we can formulate a mathematical expression of the First Law for a process. Knowing that the total energy of a system at any point in time (E) is the sum of the kinetic energy, potential energy and internal energy (equation (8.4)), we can also say that any change in energy of the system must correspond to changes in these energies, or:
Further, because \(\Delta E\) can only change via heat or work interactions we can also say,
where \(Q_{\rm net}\) and \(W_{\rm net}\) represent the net heat or work transfers to or from the system. That is, there can be multiple forms of heat transfer or work, but they are all captured here with this simple expression, which we typically call the energy conservation equation, or energy equation. The negative sign is a matter of convention that will be useful when evaluating complex systems, and is a result of the fact that we attribute ALL heat transfer to the system as a positive quantity and from the system as a negative quantity, and ALL work interactions the opposite way - i.e., to the system as a negative quantity and from the system as a positive quantity. There is a historical basis for this that derives from the fact that heat engines were designed to take in heat and output work, thus those terms were always treated positively. And while the sign convention is arbitrary, it is important to remain consistent when evaluating property values using this equation. Further, this convention is appled only when adding numerical values of \(Q\) and/or \(W\) to the energy equation. If solving for \(Q\) or \(W\), the resulting sign will be indicative of the direction of energy transfer.
At first introduction this can seem confounding, but as long as you always use equation (8.6) consistently and treat heat inputs and work outputs as positive terms, and heat outputs and work inputs as negative terms, the First Law will be satisfied. It can be thought of similarly to balancing a budget, where the budget is now energy, instead of dollars, and the inputs and outputs are heat and work instead of debits and credits. Refer to Figure 5.1 below which shows an arbitrary system with multiple heat transfer and work terms, labled with subscripts 1 and 2, with varying direction indicating to or from the system. We can see that if we apply the rules discussed above that the resulting energy conservation equation reduces to \(\Delta E = (Q_1 - Q_2) - (W_2 - W_1)\). Notice that the original negative sign remains intact - positive or negative signs are only applied to the terms themselve while the negative sign in the equation remains unchanged (8.6).
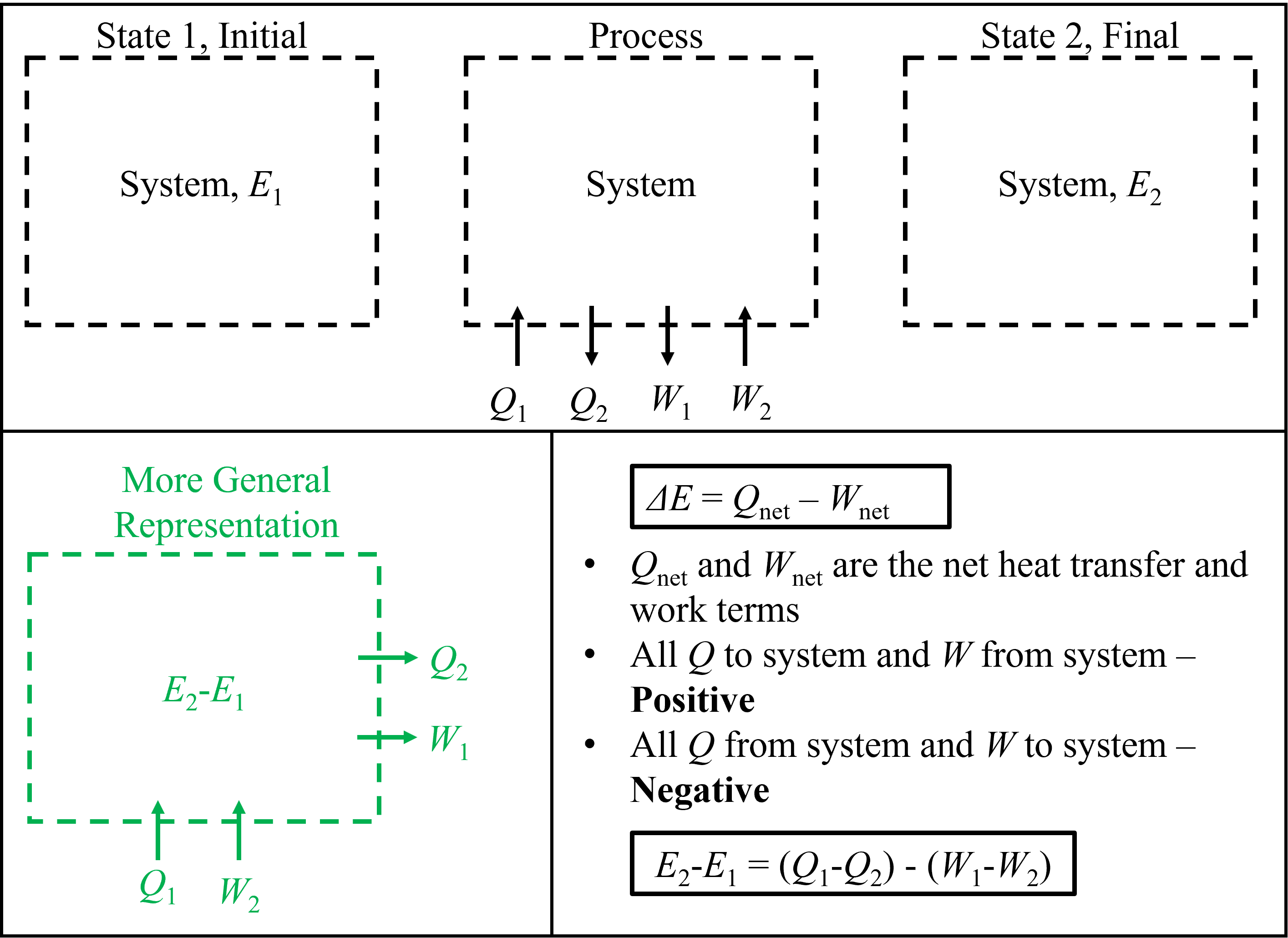
Fig. 5.1 Top) Schematic showing generic system at initial state, then undergoing process via heat and work interactions, to arrive at a final state. Bottom Left) The typical representation of the system undergoing a process, drawn all with one diagram. Bottom Right) Closed system energy conservation analysis for the described process.#
Again, It is important to note that applying the correct signage to heat transfer and work terms is only done when evaluating property values, for example internal energy changes. Refer to Figure 5.2 below which shows the same system as above, but this time numerical values for the heat transfer and work terms have been provided. Pay careful attention to the signs that are applied.
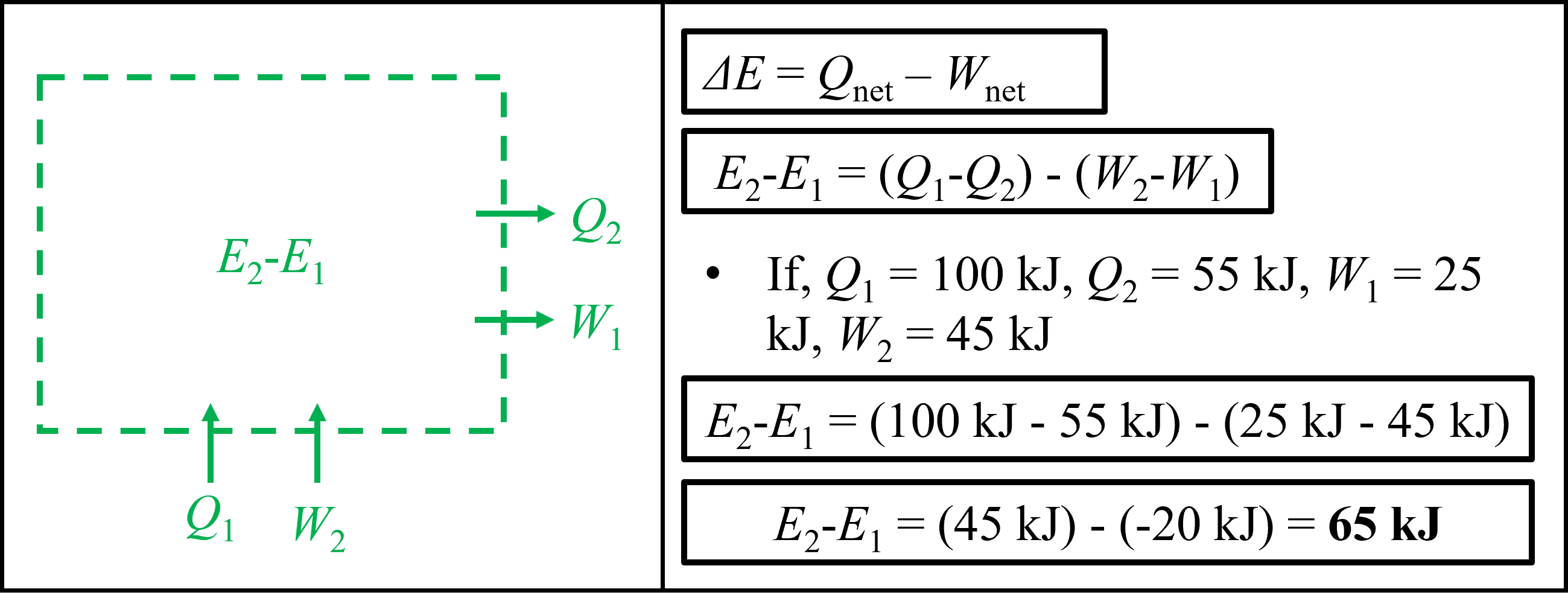
Fig. 5.2 Representation of a system undergoing a process with multiple heat transfer and work terms. On the right are assigned numberical values for each term - notice how they are applied in the energy conservation equation to arrive at the final determination for the change in energy of the system.#
If the goal is to determine \(Q\) or \(W\) via evaluation of the energy equation, then no modification of the signs is needed. The resulting sign will indicate the direction of the energy transfer. For example, see below Figure 7.3 where the net work was determined to be 40 kJ, indicating that work had to be done by the system system.

Fig. 5.3 Representation of a system undergoing a process where the net work is to be determined. Upon solving for \(W_{\rm net}\), the resulting sign indicates the direction of work. In this example, because the net work is positive, work was done by the system.#
Often, the thermodynamic system under consideration is stationary, in which case the kinetic energy and potential energy terms can be neglected. Thus, the most typical form of the closed system energy conservation equation for a process going from one thermodynamic equilibrium state to another is related to the change in internal energy.
We can also express the First Law for closed systems in differential form, as:
Recall the symbol \(\delta \), which represents an inexact differential and integration depends on the path that is taken. And upon differentiation with respect to time we arrive at the rate form of the energy conservation for a stationary, closed system.
Where
Notice the dot overheat the heat transfer and rate terms. The dot indicates that it is per unit time, for example \(\frac {\rm kJ}{\rm s}\) or \(\rm W\). This will be encountered often whenever we are dealing with transient systems, i.e., not steady state, and we apply the same rule to properties that are changing with time. For example, the mass per unit time is the mass flow rate, or \(\dot m\) and the specific volume per unit time is the specific volumetric flowrate \(\dot v\).
5.2.1. Heat Transfer#
Heat transfer to or from the system may occur via conduction, convection or radiative heat transfer. We will typically treat heat transfer as an energy source or sink to the system without consideration of the mechanism, but a brief discussion of each mode follows. A thorough discussion is beyond the scope of this text, but detailed discussion in any undergraduate heat transfer textbook, for example…, will cover these topics in more detail. Heat transfer will only spontaneously occur in the direction of high temperature to low temperature, as a result of the Second Law of Thermodynamics (discussed later). This implies that heat will always flow from a warm mug of coffee, thus decreasing the temperature of the coffee and simultaneously increasing the temperature of the surroundings. The reverse scenario, heat transfer from lower temperature surroundings to a warm cup of coffee, resulting in heating of the coffee and cooling of the surroundings, is impossible.
Figure 5.4 above schematically depicts the different modes of heat transfer through a solid via conduction, and from the surface of the solid via convection and radiation. If the bottom surface T1 is higher than the top surface T2, conduction heat transfer will occur in the direction from high to low temperature. The rate of convective heat transfer is dictated by the difference between the surface temperature and the surrounding temperature. The intermediate region where the temperature decreases from the surface to the surroundings is called the boundary layer and has important implications in fluid dynamics and heat transfer, but are beyond the scope of this text. Radiative heat exchange will occur equally in all directions if the surface is a diffuse emitter.
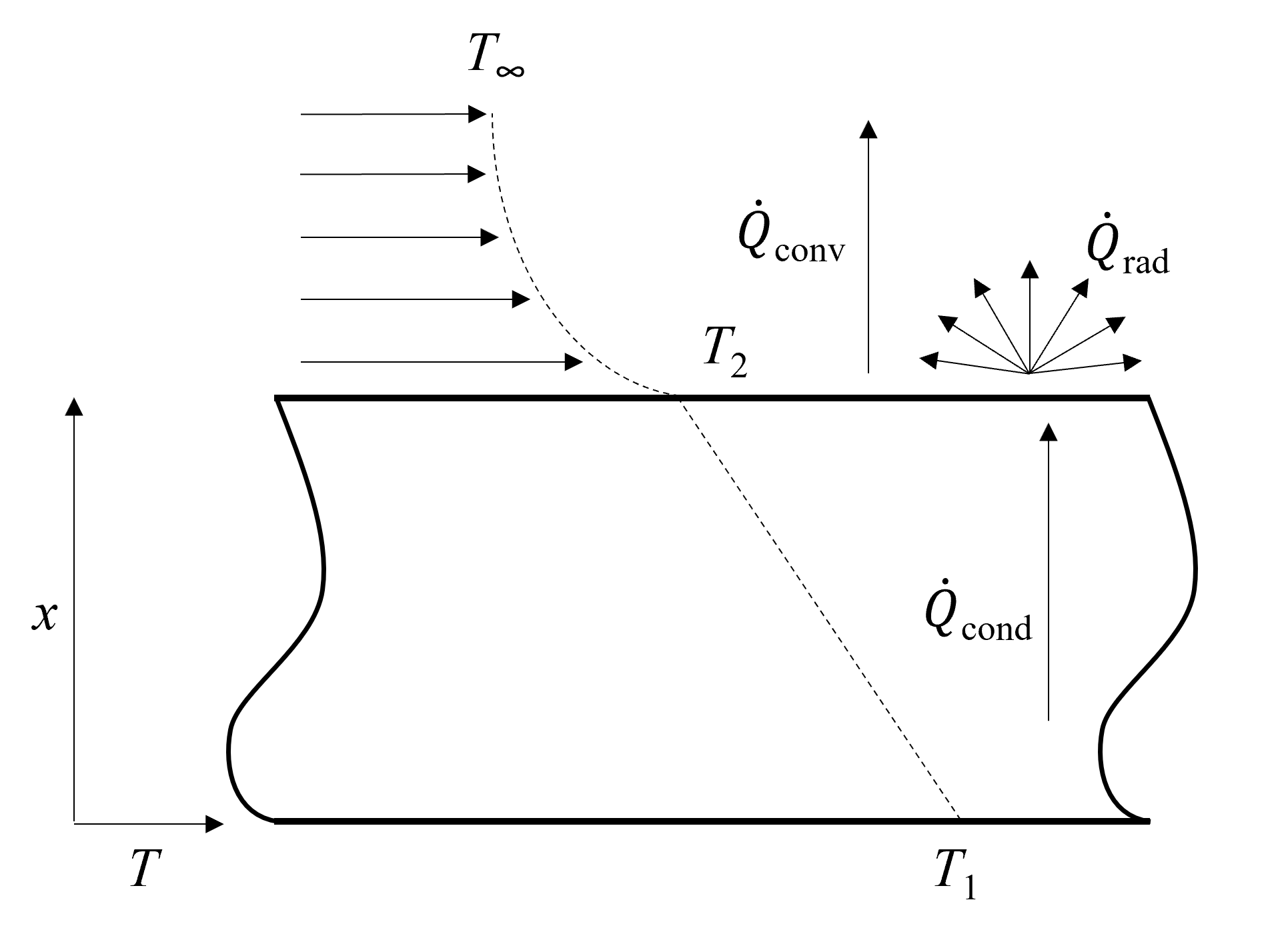
Fig. 5.4 Schematic depicting conductive, convective and radiative heat transfer modes.#
5.2.1.1. Conduction Heat Transfer#
Conductive heat transfer is a result of electron and phonon transport in a medium, and is usually the dominant mode of heat transfer in a solid. The one-dimensional, steady state rate of conductive heat transfer (\(\dot{Q}_{\rm cond}\)) is related to the thermal conductivity (\(k\)) which is a material dependent property, the cross sectional area (\(A\)), and the temperature gradient between top and bottom surfaces of the medium through which heat is being conducted.
For example, for conductors such as metals, \(k\) is high, whereas for insulators it is low. Often, \(k\) is assumed to be independent of temperature, in which case we can replace the differentials with differences.
The negative sign is applied only to ensure (\(\dot{Q}\)) remains a positive quantity, because the temperature graident increasing in the x-direction is negative as a result of heat transfer always occuring in the direction of high temperature to low temperature.
5.2.1.2. Convective Heat Transfer#
Convective heat transfer is usually the dominant mode for fluids (i.e. gases and liquids) and occurs as a result of bulk movement of the fluid. The steady state convective heat transfer rate (\(\dot{Q}_{\rm conv}\)) is related to the convective heat transfer coefficient (\(h\)), the cross sectional area (\(A\)) where the heat transport occurs, and the difference between the surface temperature (\(T_s\)) and fluid temperature far from the surface (\(T_\infty\)).
The convective heat transfer coefficient is a parameter that is related to the fluid properties and the specific flow situation (e.g. fluid velocity, turbulance, etc.).
5.2.1.3. Radiative Heat Transfer#
Radiative heat transfer occurs as a result of electromagnetic wave propogation from one surface to another, either through a vacuum or a medium. Radiative heat transfer is the only mode of heat transfer that does not require a medium to propogate, and is thus the only mode of heat transfer to occur in vacuum. Propogation through a vacuum is unmitigated and thus we feel the effects of the electromagnetic radiation emitted by the sun even from millions of miles away. The net radiative heat transfer rate (\(\dot{Q}_{\rm rad}\)) between two surfaces with identical emissivities (\(\varepsilon\)), a surface property of the material that varies from 0 to 1, at different temperatures \(T_1\) and \(T_2\) is described mathematically below.
where \(\sigma\) is the Stefan-Boltzmann constant and equal to 5.67 E-8 \(\frac{\rm W}{\rm m^2K^4}\). Because of the fourth order temperature dependence, radiative heat transfer is often the dominant heat transfer mode at elevated temperature. Often, at lower temperatures the magnitude is small compared to convection and conduction, but not always.
5.2.2. Work Interactions#
5.2.2.1. Mechanical Work#
A typical type of work often encountered in thermodynamic systems is mechanical work (\(W_{\rm mech}\)). Mechanical work is performed any time an external force (\(F_{\rm ext}\)) acts through a distance, or
where the integration limits 1 and 2 represent the initial and final positions through which the force was applied. In the case of non-stationary systems where \(KE\) and \(PE\) cannot be ignored, the work associated with changing velocity or height can be determined with this expression. For example, in the case of \(KE\) the force can be expressed as \(ma\) and thus removing the mass outside the integral, the inside becomes \(\frac {dV}{dt} dx\), or \(VdV\) (i.e., \(V = \frac {dx}{dt}\)). Integrating from position 1 to 2 we see that the mechanical work required to change the velocity of an object with constant mass is the following.
In the case of gravitational \(PE\) the force can be expressed as \(mg\), and thus integrating between heights 1 and 2 (\(\int_{1}^{2} mgdx\)), we see that the mechanical work required to change the elevation of an object with constant mass is the following.
In the case of closed thermodynamic systems, boundary work is especially relevent. Boundary work is a type of mechanical work that is relevant whenever the volume of a system changes due to expansion or compression, for example in the case of a piston-cylinder device. Starting from (8.12), we can relate the volume of a system to its position by dividing by its cross sectional area, \(A\) - i.e. \(dx = \frac {dV}{A}\). Then, recognizing the relationship between force and pressure, i.e., \(p = \frac {F}{A}\), we can rearrange equation (8.12) in the form below,
where the integration limits 1 and 2 now represent the initial and final volumes during compression and expansion processes. It should be noted that this derivation is only valid for slow, or reversible processes, where the internal and external forces, are quasi-equal. I.e., the internal pressure is in equilibrium with the external force being applied. More on this is discussed in the next chapter in the section Section 6.1 More on Boundary Work - Reversible Processes.
Note that for a constant pressure processes, the boundary work reduces to:
Other forms of mechanical work include rotational (or shaft) work, flow work, spring work, work done on elastic solid bars and that associated with the stretching of liquid films. Flow work, which is related to the work required to push flow into and out of control volumes, will be especially important during our consideration of open systems.
5.2.2.2. Other Types of Work#
In addition to mechanical work, there are several other forms of work inluding electric work, magnetic work and electrical polarization work that will not be considered in detail here. But, for the sake of their application towards the First Law, we can treat these simply as work terms either to or from our system of interest, being sure to apply to correct signage.
5.2.2.3. Path Dependence#
In differental form, boundary work is expressed as the following,
where the use of \(\delta\) refers to the fact that this is an inexact differential and its evaluation is dependent on the path of the process. Recall discussion of Figure 3.1 in Section 3.1 Thermodynamic Systems. I.e., the boundary work depends on the volume dependence of pressure and to evaluate we would need to know the functional dependence of pressure on volume, or \(p(V)\). We will see later after our introduction of the Second Law of Thermodynamics that we can also relate the reversible heat transfer to temperature and entropy via a similarly formed expression.
5.2.2.4. Example - Constant Volume System#
Initially, a constant volume, 1m\(^3\) system, composed of H2O is at 20 \(^\circ\)C and 100 kPa. Calculate the final internal energy and temperature after 20 kJ of heat have been added.
Solution - First we should recognize that this is a stationary, closed system and the volume remains constant. Because it is stationary we can neglect changes in kinetic and potential energies, and because the volume remains constant we can neglect any boundary work. Therefore, the closed system energy conservation equation reduces to:
\(\Delta U = Q\) and therefore \(U_2-U_1\) = 20 kJ. Notice that the heat transfer term remained positive because heat was added to the system. We can use Cantera to help us find property values, \(v_1\) and \(u_1\) at State 1.
import cantera as ct
species1 = ct.Water()# define state 1 as water
species1.TP = 273.15+20, 100000
v1=species1.UV[1]
print(v1) #units m^3/kg
u1=species1.UV[0]
print(u1) #units kJ/kg
0.0010017390901042916
-15886873.004300132
Knowing \(v_1\) and the total volume we can solve for the mass, \(m\), and then subsequently \(U_1\). Then we can directly solve for \(U_2\) using the energy equation.
m=1/v1
U1 = u1*m
U2 = 20+U1
print(U2) # units J
-15859292246.05916
Then we can also determine the temperature at State 2, recognizing that the specific volume remains the same and \(u_2 = \frac {U_2}{m}\)
species1.UV = U2/m,v1
T2=species1.TP[0]
print(T2) #units in K
293.15
5.2.2.5. Example - Constant Pressure System#
Initially, a piston-cylinder filled with nitrogen gas (N2) with volume 1m\(^3\) is at 20 \(^\circ\)C and 100 kPa. Then, heat is added and the piston expands as a result until the temperature reaches 80 \(^\circ\)C. Calculate the heat transfer and work for this process.
Solution - First we should recognize that this is a stationary, closed system and the volume is not constant. Because it is stationary we can neglect changes in kinetic and potential energies, but we cannot neglect the boundary work because the volume changes. Therefore, the closed system energy conservation equation reduces to:
\(\Delta U = Q - W\), where \(W = p \Delta V\) or \(W = pm(v_2-v_1)\). We can solve for properties at State 1 and State 2 since we know both pressure and temperature at each state. Therefore, we can first solve for the boundary work. Then, knowing the boundary work we can use this to solve for the heat transfer using the energy equation. We can use Cantera to help us find property values at each state.
import cantera as ct
#First State 1
species1 = ct.Nitrogen()# define state 1 as nitrogen
species1.TP = 273.15+20, 100000
v1=species1.UV[1]
print(v1) #units m^3/kg
u1=species1.UV[0]
print(u1) #units J/kg
0.8698356662951862
-92360.7771094957
#Now State 2
species1.TP = 273.15+80, 100000 #redefine temperature
v2=species1.UV[1]
print(v2) #units m^3/kg
u2=species1.UV[0]
print(u2) #units J/kg
1.0482602451043912
-47752.384543076914
Knowing \(v_1\) and the initial total volume we can solve for the mass, \(m\), and finally the work
m=1/v1
print(m) # units kg
W=100*m*(v2-v1) #notice units. Multiplied by a pressure of 100 kPa, thus units for work are kJ
print("Boundary Work is ", W, "kJ")
1.1496424425307958
Boundary Work is 20.512446858974297 kJ
Then we can solve for the heat transfer during the process using the energy equation, or \(\Delta U = Q - W\). And rearranging to solve for \(Q\) we see that \(Q = W + m(u_2-u_1)\). Because the work is done by the system we insert the boundary work as a positive value. We need to be sure that our units are consistent. Our work was in kJ and specific internal energies in J/kg, so we will divide the internal energy terms by 1000 so that the units are kJ/kg.
Q = W + m*(u2/1000-u1/1000)
print("The Heat Transfer is ", Q, "kJ")
print("or with less significant digits")
print("The Heat Transfer is ", round(Q,2), "kJ")
The Heat Transfer is 71.79614824640458 kJ
or with less significant digits
The Heat Transfer is 71.8 kJ
5.3. Enthalpy#
You may have noticed if you typed \(species1()\) into your jupyter notebook during the prior example that the specific property enthalpy (\(h\)) is shown right above internal energy. See below.
species1()
nitrogen:
temperature 353.15 K
pressure 1e+05 Pa
density 0.95396 kg/m^3
mean mol. weight 28.013 kg/kmol
vapor fraction 1
phase of matter supercritical
1 kg 1 kmol
--------------- ---------------
enthalpy 57074 1.5988e+06 J
internal energy -47752 -1.3377e+06 J
entropy 7016 1.9654e+05 J/K
Gibbs function -2.4206e+06 -6.781e+07 J
heat capacity c_p 1041.5 29176 J/K
heat capacity c_v 743.77 20836 J/K
Enthalpy (\(H\)) is an extensive property of a system that is related to the internal energy and boundary work, with units, J. Specific enthalpy is a property that is tabulated primarily for convenience. Whenever a piston-cylinder expands in a constant pressure process, we can re-write the energy equation like below becuase the boundary work reduces to \(p \Delta V\).
Rearranging the above equation, we can solve for the heat transfer as:
The terms \(U + pV\) occur often enough in thermodynamic processes that these have also been tabulated, and we call this enthalpy. Thus,
and for constant pressure processes the heat transfer is therefore the change in enthalpy.
Thus, the change in enthalpy accounts for the changes in internal energy and boundary work of the system. Recall, that for constant volume processes the heat transfer is the change in internal energy, as a result of zero boundary work.
Let’s revisit the constant pressure piston-cylinder example above and see how we could solve this more simply using enthalpy, rather than requiring evaluation of internal energy and volume.
5.3.1. Example Revisted - Constant Pressure System using Enthalpy#
Initially, a piston-cylinder filled with nitrogen gas (N2) with volume 1m\(^3\) is at 20 \(^\circ\)C and 100 kPa. Then, heat is added and the piston expands as a result until the temperature reaches 80 \(^\circ\)C. Calculate the heat transfer for this process.
Solution - First we should recognize that this is a stationary, closed system and the volume is not constant. Because it is stationary we can neglect changes in kinetic and potential energies, but we cannot neglect the boundary work because the volume changes. Therefore, the closed system energy conservation equation reduces to:
\(\Delta U = Q - W\), where \(W = p \Delta V\) or \(W = pm(v_2-v_1)\). But, because this is a constant pressure process, we also know that the heat transfer is the change in enthalpy, or \(Q = \Delta H = m(h_2-h_1)\). Therefore, we can solve for the heat transfer by evaluating the specific enthalpy at each state, without having to determine anything related to the boundary work. We can solve for specific enthalpies at State 1 and State 2 since we know both pressure and temperature at each state. Then, we can determine the specific volume at State 1 and knowing that and the initial volume we can solve for the mass of the system. We can use Cantera to help us find property values at each state.
import cantera as ct
#First State 1
species1 = ct.Nitrogen()# define state 1 as nitrogen
species1.TP = 273.15+20, 100000
v1=species1.UV[1]
print(v1) #units m^3/kg
h1=species1.HP[0] # note that the .HP is used to get or set property values and needed for enthalpy
print(h1) #units J/kg
0.8698356662951862
-5377.210471401646
#Now State 2
species1.TP = 273.15+80, 100000 #redefine temperature
h2=species1.HP[0]
print(h2) #units J/kg
57073.6399838529
Knowing \(v_1\) and the initial total volume we can solve for the mass, \(m\), and finally the heat transfer.
m=1/v1
print(m) # units kg
Q=m*(h2-h1)/1000 #notice units. Divided by 1000 to convert from J/kg to kJ/kg.
print("The Heat Transfer is ", Q, "kJ")
print("or with less significant digits")
print("The Heat Transfer is ", round(Q,2), "kJ")
1.1496424425307958
The Heat Transfer is 71.7961482555043 kJ
or with less significant digits
The Heat Transfer is 71.8 kJ
Notice that the answer is identical to the prior example, when we used both internal energy and boundary work to determine the heat transfer. But in this case there was one fewer step because we did not need to evaluate the boundary work. Of course, we could also determine the boundary work without ever calculating the change in volume by understanding that we can also solve for the internal energies at states 1 and 2. With this and the heat transfer we could solve directly for the boundary work using the energy conservation equation, \(W = Q - \Delta U\).
5.3.2. Exercise 3#
A closed rigid container of 0.5 m3 is placed on a hot plate. Initially it contains a two phase mixture of saturated liquid and saturated vapor H2O at \(p_1\) = 1 bar with x = 0.5. After heating \(p_2\) = 1.5 bar. Determine T at states 1 and 2. Determine the heat transfer during the process.
A piston cylinder assembly initially (State 1) contains 10 kg of H2O at 1200 kPa.
If 8 kg is in the liquid form and the rest vapor, determine the temperature, specific volume and specific enthalpy.
The cylinder continues to be heated at constant pressure until the temperature reaches 300 °C (State 2). Determine the final state (compressed liquid, saturated mixture, superheated vapor), specific volume and specific enthalpy.
Determine the heat transfer and work for this process.
Water initially at 200 kPa and 300 °C is contained in a piston-cylinder fitted with stops. The water is allowed to cool at constant pressure until it exists as a saturated vapor and the piston rests on the stops. Then, the water continues to cool until the pressure is 100 kPa. Find:
The change in specific internal energy during initial cooling to the stops
The change in specific volume during initial cooling to the stops
The change in specific enthalpy during initial cooling to the stops
The specific heat transfer during initial cooling to the stops, using answers from parts a and b.
The specific heat transfer during initial cooling to the stops, using answer from part c.
The change in specific internal energy during final cooling while resting on the stops
The total specific heat transfer during the entire process
A piston-cylinder contains 0.005 m3 of liquid water and 0.9 m3 of water vapor at 600 kPa. Heat is transferred at constant presssure until the temperature reaches 200 °C.
Determine the heat transfer using enthalpies
Determine the heat transfer without using enthalpies
A 1-m3 tank containing air at 10°C and 350 kPa is connected through a valve to another tank containing 3 kg of air at 35°C and 150 kPa. Now the valve is opened, and the entire system is allowed to reach thermal equilibrium with the surroundings, which are at 20°C. Determine the volume of the second tank and the final equilibrium pressure of air.
A mass of 0.1 kg of helium fills a 0.2 m3 rigid vessel at 350 kPa. The vessel is heated until the pressure is 700 kPa. Calculate the temperature change of helium as a result of this heating.
Determine the specific volume of refrigerant-134a vapor at 0.9 MPa and 70°C based on (a) the ideal-gas equation and (b) using Cantera.
Carbon dioxide gas enters a pipe at 3 MPa and 500 K at a rate of 2 kg/s. CO2 is cooled at constant pressure as it flows in the pipe, and the temperature of the CO2 drops to 450 K at the exit. Determine the volume flow rate and the density of carbon dioxide at the inlet and the volume flow rate at the exit of the pipe using (a) the ideal-gas equation and (b) using Cantera.
A rigid 10-L vessel initially contains a mixture of liquid water and vapor at 100°C with 12.3 percent quality. The mixture is then heated until its temperature is 180°C. Calculate the heat transfer required for this process.
Two tanks (Tank A and Tank B) are separated by a partition. Initially Tank A contains 2 kg of steam at 1 MPa and 300°C while Tank B contains 3 kg of saturated liquid–vapor mixture at 150°C with a vapor mass fraction of 50 percent. The partition is now removed and the two sides are allowed to mix until mechanical and thermal equilibrium are established. If the pressure at the final state is 300 kPa, determine (a) the temperature and quality of the steam (if mixture) at the final state and (b) the amount of heat lost from the tanks.
A 3 m3 rigid tank contains hydrogen at 250 kPa and 550 K. The gas is now cooled until its temperature drops to 350 K. Determine (a) the final pressure in the tank with and without using the ideal gas law (i.e., Cantera property evaluation) and (b) the amount of heat transfer with and without using specific heats (i.e., Cantera property evaluation).
A piston is filled with nitrogen at T = 700 K and v = 0.4 m3/kg. The piston then compresses at a constant pressure until T = 500 K.
What is the work (W) per kg of nitrogen done by the piston, assuming there is no heat transfer?
The piston is then held in place and the nitrogen is heated 20°C, what is the pressure (P) and heat transfer per kg (q) of the heating?
A 0.4 kg of water at 800 K fills a 20L tank. It undergoes a constant pressure process, where it cools until the temperature of the water is half of its original value. Find the heat transfer from this process (Q).
CO2 at v = 0.45 m3/kg is heated 100°C in a piston. The piston head has a mass of 10kg and a 1 cm diameter. The piston head is free to move. What is the specific heat transfer (q) during this process? (The values for pressure on Cantera is absolute pressure)
A rigid tank is filled with 100L of water at ambient conditions. 300 kJ of heat are transferred to the water by a natural gas heater. What is the final pressure (P) and temperature (T) in the tank after the heating process?
A 50L tank of water at ambient conditions is sealed and placed under the sun for five hours. 100 kJ of heat are transfered to the tank. Assume the water does not reach the stagnation temperature. What is the temperature (T) and pressure (P) of the water after heating?
